The Meij Theorem

Context

This theorem plays a small but important part in my projection method of a 3D model to the screen. See the Functional description of tree package, which is part of the documentation accessible from the documentation link on the home page.

Theorem

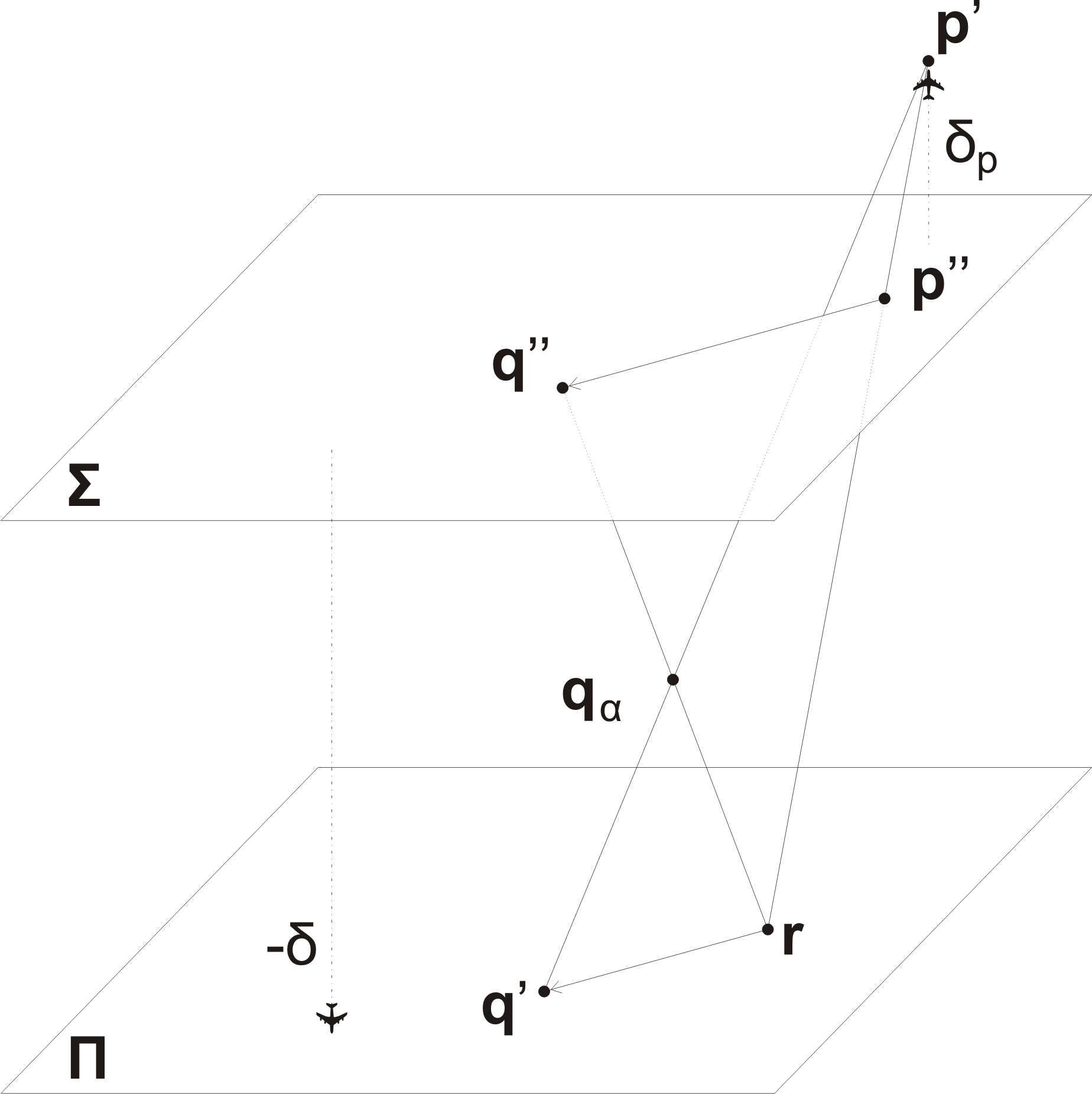
Let Σ and Π be two planes at a distance δ > 0, let r and q' be vectors on the Π plane and let p' be a vector which is on the same side of Π as Σ. Let p'' be the intersection of the line from r to p' with the Σ plane.
Define q_α = p' + α (q' - p') with 0 <= α < 1.
Let q'' be the intersection of the line from r to q_α with the Σ plane.
Then q'' - p'' = c (q' - r) for some c >= 0.

Proof

Consider an orthonormal base such that (x, y, z) = (x, y, -δ) for the Π plane and (x, y, z) = (x, y, 0) for the Σ plane.

Let δ_p be the distance that we have to travel to get from the Σ plane to p' so δ_p can be negative but at least δ_p > - δ.

Since p'' = p' + λ (r - p') is in the Σ plane, taking the z coordinates:

δ_p + λ (-δ - δ_p) = 0 so λ = δ_p / (δ + δ_p). It follows that p'' = p' + δ_p / (δ + δ_p) (r - p').

Consider q_α = p' + α (q' - p'). We search q'' = q_α + λ (r - q_α) in the Σ plane, or (p' + α (q' - p')) + λ (r - (p' + α (q' - p'))) in the Σ plane. Again, taking the z coordinates:

(δ_p + α (-δ - δ_p)) + λ (-δ - (δ_p + α (-δ - δ_p))) = 0 so λ = (δ_p - α (δ + δ_p)) / ((1 - α) (δ + δ_p)).

Now we can express q'' in terms of p', q' and r using only constants and α, δ and δ_p. If you do this you will find that

q'' = δ / (δ + δ_p) p' +
+ α δ / ((1 - α) (δ + δ_p)) q' +
+ (δ_p - α (δ + δ_p)) / ((1 - α) (δ + δ_p)) r

Likewise

p'' = δ / (δ + δ_p) p' +
+ δ_p / (δ + δ_p) r

So q'' - p'' = α δ / ((1 - α) (δ + δ_p)) (q' - r)

which is what we set out to prove.